近日，南方科技大学数学系、杰曼诺夫数学中心讲席教授Stavros Garoufalidis团队在计算双曲3-流形中不可压缩表面方向上取得重大进展，论文“Counting essential surfaces in 3-manifolds”在国际顶级数学期刊之一Inventiones Mathematicae上在线发表。

双曲3-流形被认为是可能的宇宙形状，在过去的70多年中，基本面在双曲3-流形拓扑研究中一直起关键中心作用。曾有研究表明，如果不能简化，则双曲3-流形中的表面是不可压缩的。菲尔兹奖获得者Thurston在80年代的开创性工作表明，具有不可压缩表面的流形满足几何化猜想。2003年，由菲尔兹奖获得者 Perelman解决了这个猜想。但是，双曲3-流形到底有多少个不可压缩表面？这仍然是一个公开问题。

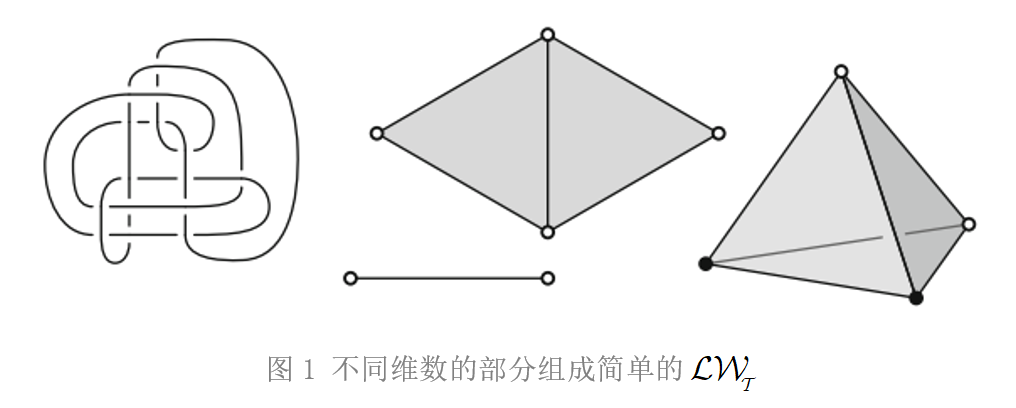
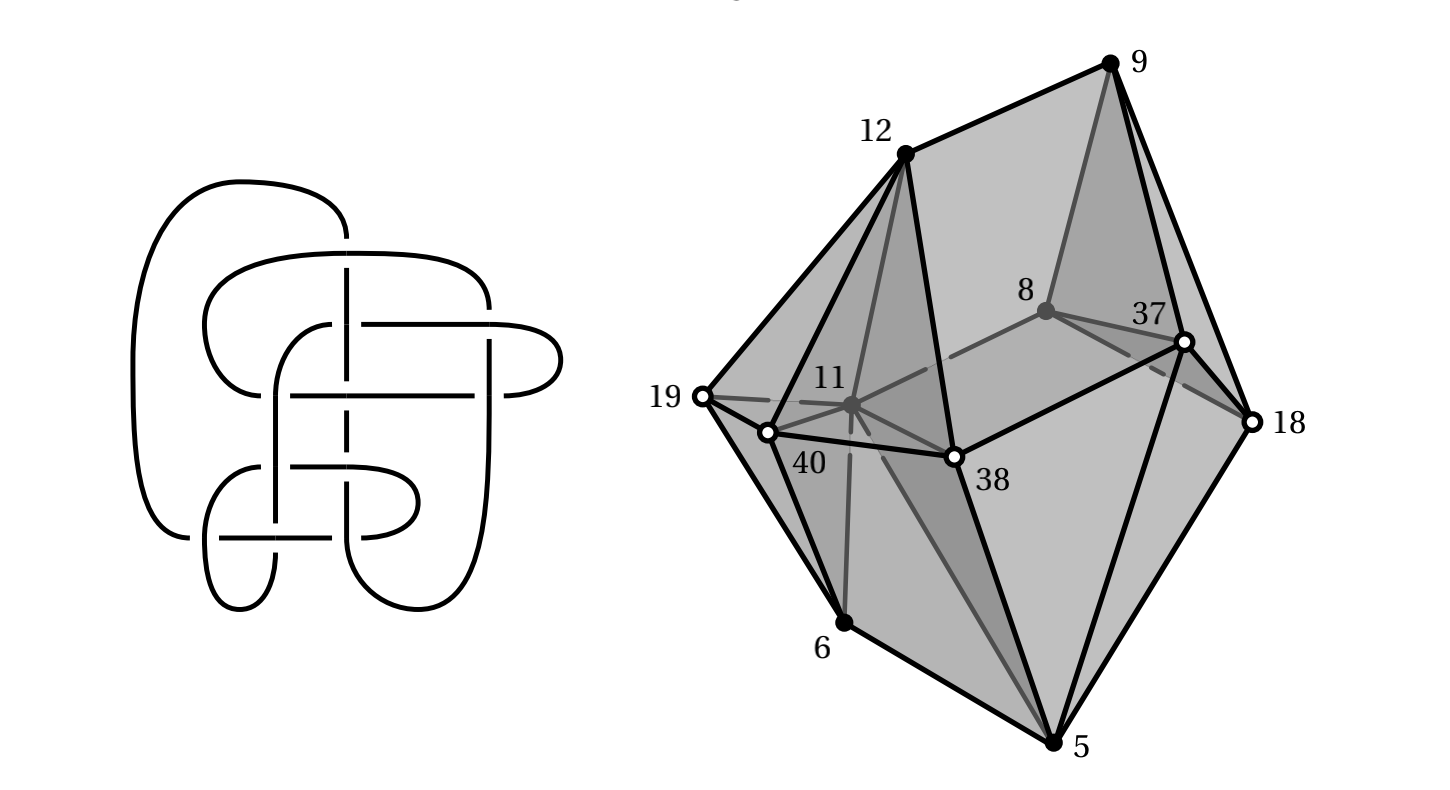
图2  Conway 结形成的复杂三维复合体

    如图1、图2所示，Stavros Garoufalidis教授团队就双曲3-流形中基本面的合痕类计数问题进行了研究，重点关注了广泛类别的双曲3-流形中的闭合基本表面。他们证明用欧拉示性数对基本面的计数总有短生成函数，进而具有拟多项式行为，并给出了这些基本面个数的精确公式和渐进性，所给出的算法还可以计算这些生成函数和相应的曲面。此外，Stavros Garoufalidis教授团队还通过使用双曲3-流形的SnapPea数据库，揭示了近60000个流形的计数结构，并利用孔数量对不可压缩表面进行计数。图3、图4显示了此类计数的统计图。

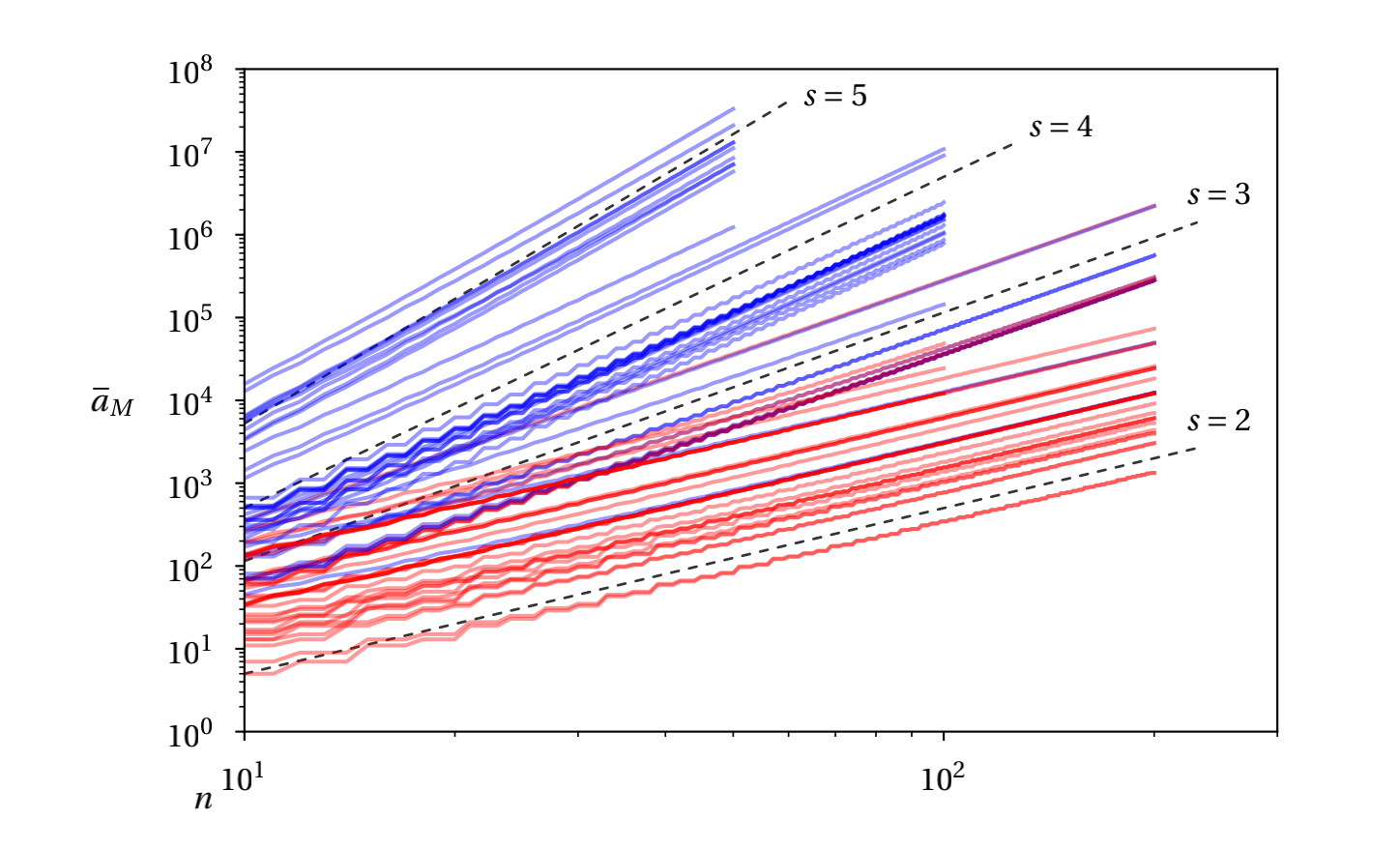
图3

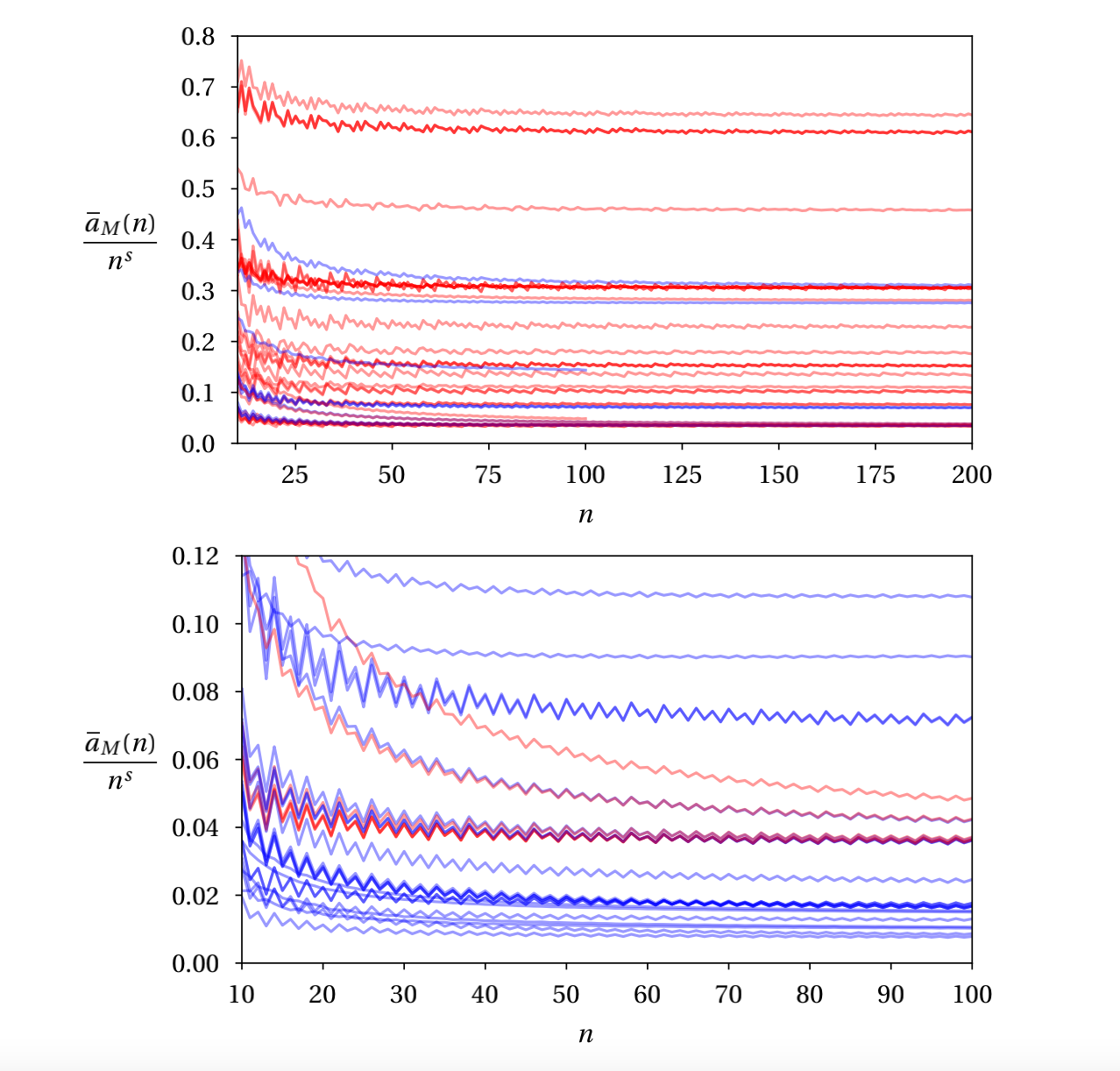
图4

   值得一提的是，虽然不可压缩曲面的计数是三维拓扑和几何问题，但它与量子拓扑问题有关。例如Davide Gaiotto和Sergei Gukov，Tudor Dimofte的超对称3D指数，其物理定义涉及超对称、量子场论、膜量子化和M理论的思想。Stavros Garoufalidis教授在与澳大利亚和美国的研究人员多次合作中，发现了不可压缩表面和3D指数之间的联系。

Stavros Garoufalidis

Stavros Garoufalidis教授先后在麻省理工学院、布朗大学、哈佛大学等多所高校任职，他的研究方向为低维拓扑、几何与数学物理， 曾获得斯隆青年学者论文奖、约翰·西蒙·古根海姆奖、美国数学学会百年纪念成就奖等荣誉。自2019年全职加入南方科技大学以来，他为南科大数学学科的发展和人才培养作出重要贡献，此次的研究成果助推了我校数学学科的建设。

伊利诺伊大学教授NathanDunfield和墨尔本大学教授HearRubinsetin为该论文共同作者。

论文链接：https://link.springer.com/content/pdf/10.1007/s00222-021-01090-w

来源：南方科技大学新闻网